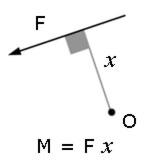
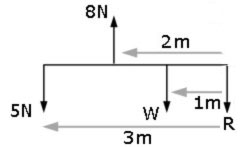
Newton ‘s law of gravitation states that the force of attraction between particles is directly proportional to their mass and inversely proportional to the square of distance apart.
Where G is the universal gravitational constant,
7.2 GRAVITATIONAL FIELD STRENGTH
• A gravitational field is a region where gravitational force acts on massive bodies. Eg . gravitaional field of the Earth.
• The gravitational field strength tells us how strong a gravitational field is. The gravitational field strength of the Earth near its surface is 9.81m / s2.
• The gravitational field strength , E at a point is the force of gravity per unit mass exerted on a mass placed.
The variation of the acceleration due to gravity g’ with distance r from the centre of the Earth is illustrated by the graph above.
7.3 Gravitational Potential
• The strength of the gravitational force at a point in a gravitational field is described by the gravitational field strength E or g is a vector quantity.
• Another quantity associated with the point in the gravitational field is the gravitational potential. It is a scalar quantity.
• The gravitational potential V at a point P in a gravitational field is defined as the work done per unit mass to bring a body from infinity to P. The unit for gravitational potential is Jkgˉ¹.
• The gravitational potential energy U of a body at a point P in a gravitational field is defined as the work done to bring the body from infinity to P. The unit for gravitational potential energy is J.
• Hence the gravitational potential energy U of a body of mass m at a point where the gravitational potential, V is given by
U = mV
• On the surface on the Earth, r = R
– Gravitational potential, V = -
– Gravitational potential energy, U = -
– The graph illustrates the variation of the gravitational potential V with distance r from the centre of the Earth.
7.4 RELATIONSHIP BETWEEN g AND G
-G is the Universal Gravitational Constant.
- It is a scalar quantity with dimension
- g is the acceleration due to gravity . - It is a vector quantity with dimension
 Where g = acceleration due to gravity
Where g = acceleration due to gravity R = constant radius of earth
G = universal gravitational constant
M = mass of Earth
7.5 Satellite Motion in Circular Orbits
Satellite is a body that revolves round a planet. Satellites can be categorized as natural satellites or man-made satellites. The moon, the planets and comets are examples of natural satellites. Examples of man-made satellites are Sputnik I , Measat I ,II and III which are communication satellites. In order to launch satellite into orbit , rockets are used. When rocket that carries the satellite reaches the required height , the satellite is launched into circular orbit with a certain velocity v that is tangential to intended orbit.
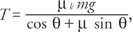 solving for T.
solving for T.